5  Exploratory Data Analysis

5.1 Intro

This chapter will show you how to use visualization and transformation to explore your data in a systematic way, a task that statisticians call exploratory data analysis, or EDA for short. EDA is an iterative cycle, where you should feel free to “fall in love” with your data.

You:

1. Generate questions about your data.

2. Search for answers by visualizing, transforming, and modelling your data.

3. Use what you learn to refine your questions and/or generate new questions.

Note: EDA is not a formal process with a strict set of rules!

See Wickham, Çetinaka-Rundel, and Grolemund (2017) for more, in particular the EDA chapter.

Do it yourself with R

Copy the script ExploratoryDataAnalysis.R and paste it in your session.
Run each line using CTRL + ENTER

5.2 Load packages

library(tidyverse) # Pack of most used libraries for data science
library(skimr) # summary of the data
library(DataExplorer) # exploratory data analysis
library(corrplot) # correlation plots

5.3 Dataset

The database used in this example is a treated database from the Mobility Survey for the metropolitan areas of Lisbon and Porto in 2018 (INE 2018). We will only focus on trips within the metropolitan area of Lisbon.

Included variables:

• Origin_dicofre16 - Code of Freguesia (district) as set by INE after 2016 (Distrito + Concelho + Freguesia), for trip origin
• Total - number of trips with origin at each district
• Walk - number of walking trips
• Bike - number of bike trips
• Car - number of car trips. Includes taxi and motorcycle.
• PTransit - number of Public Transit trips
• Other - number of other trips (truck, van, tractor, aviation)
• Distance - average trip distance (km)
• Duration - average trip duration (minutes)
• Car_perc - percentage of car trips
• N_INDIVIDUOS - number of residents (INE 2022)
• Male_perc - percentage of male residents (INE 2022)
• IncomeHH - average household income
• Nvehicles - average number of car/motorcycle vehicles in the household
• DrivingLic - percentage of car driving licence holders
• CarParkFree_Work - percentage of respondents with free car parking at the work location
• PTpass - percentage of public transit monthly pass holders
• internal - binary variable (factor). Yes: trip with same TAZ origin and destination, No: trips with different destination
• Lisboa - binary variable (factor). Yes: the district is part of Lisbon municipality, No: otherwise
• Area_km2 - area of in Origin_dicofre16, in km²

Import dataset

data = readRDS("../data/IMOBmodel.Rds")

Take a look at the dataset

View(data) # open in table
glimpse(data) # glimpse of the dataset

Rows: 236
Columns: 20
$ Origin_dicofre16 <chr> "110501", "110501", "110506", "110506", "110507", "11…
$ Total            <dbl> 35539, 47602, 37183, 42313, 30725, 54586, 57747, 6788…
$ Walk             <dbl> 11325, 3502, 12645, 1418, 9389, 2630, 20423, 3573, 62…
$ Bike             <dbl> 1309, 416, 40, 163, 1481, 168, 1406, 809, 13, 37, 3, …
$ Car              <dbl> 21446, 37727, 22379, 37337, 19654, 44611, 33044, 5225…
$ PTransit         <dbl> 1460, 5519, 2057, 3285, 201, 6963, 2477, 10534, 110, …
$ Other            <dbl> 0, 437, 63, 106, 0, 215, 396, 717, 2, 169, 3, 824, 0,…
$ Distance         <dbl> 11.779, 11.779, 9.868, 9.868, 9.600, 9.600, 12.875, 1…
$ Duration         <dbl> 23.96, 23.96, 22.78, 22.78, 23.39, 23.39, 26.89, 26.8…
$ Car_perc         <dbl> 60.34497, 79.25507, 60.18611, 88.24002, 63.96745, 81.…
$ N_INDIVIDUOS     <dbl> 44165, 44165, 59238, 59238, 46529, 46529, 64192, 6419…
$ Male_perc        <dbl> 47.66, 47.66, 47.12, 47.12, 45.54, 45.54, 46.14, 46.1…
$ IncomeHH         <dbl> 2204.32, 2204.32, 1896.05, 1896.05, 2430.43, 2430.43,…
$ Nvehicles        <dbl> 1.86, 1.86, 1.73, 1.73, 1.60, 1.60, 1.64, 1.64, 1.20,…
$ DrivingLic       <dbl> 63.03, 63.03, 65.42, 65.42, 67.05, 67.05, 72.75, 72.7…
$ CarParkFree_Work <dbl> 49.97, 49.97, 57.09, 57.09, 47.43, 47.43, 56.47, 56.4…
$ PTpass           <dbl> 11.14, 11.14, 17.12, 17.12, 18.25, 18.25, 19.73, 19.7…
$ internal         <fct> Yes, No, Yes, No, Yes, No, Yes, No, Yes, No, Yes, No,…
$ Lisboa           <fct> No, No, No, No, No, No, No, No, Yes, Yes, Yes, Yes, Y…
$ Area_km2         <dbl> 39.767414, 39.767414, 20.364310, 20.364310, 8.109861,…

str(data) # Structure of the dataset 

'data.frame':   236 obs. of  20 variables:
 $ Origin_dicofre16: chr  "110501" "110501" "110506" "110506" ...
 $ Total           : num  35539 47602 37183 42313 30725 ...
 $ Walk            : num  11325 3502 12645 1418 9389 ...
 $ Bike            : num  1309 416 40 163 1481 ...
 $ Car             : num  21446 37727 22379 37337 19654 ...
 $ PTransit        : num  1460 5519 2057 3285 201 ...
 $ Other           : num  0 437 63 106 0 215 396 717 2 169 ...
 $ Distance        : num  11.78 11.78 9.87 9.87 9.6 ...
 $ Duration        : num  24 24 22.8 22.8 23.4 ...
 $ Car_perc        : num  60.3 79.3 60.2 88.2 64 ...
 $ N_INDIVIDUOS    : num  44165 44165 59238 59238 46529 ...
 $ Male_perc       : num  47.7 47.7 47.1 47.1 45.5 ...
 $ IncomeHH        : num  2204 2204 1896 1896 2430 ...
 $ Nvehicles       : num  1.86 1.86 1.73 1.73 1.6 1.6 1.64 1.64 1.2 1.2 ...
 $ DrivingLic      : num  63 63 65.4 65.4 67 ...
 $ CarParkFree_Work: num  50 50 57.1 57.1 47.4 ...
 $ PTpass          : num  11.1 11.1 17.1 17.1 18.2 ...
 $ internal        : Factor w/ 2 levels "Yes","No": 1 2 1 2 1 2 1 2 1 2 ...
 $ Lisboa          : Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 2 2 ...
 $ Area_km2        : num  39.77 39.77 20.36 20.36 8.11 ...

5.4 Summary statistics

Have an overview of the variables and their statistics’ summary.

summary(data) # Check the summary statistics

 Origin_dicofre16       Total             Walk              Bike        
 Length:236         Min.   :   361   Min.   :    0.0   Min.   :   0.00  
 Class :character   1st Qu.:  5918   1st Qu.:  763.2   1st Qu.:   0.00  
 Mode  :character   Median : 17474   Median : 3125.0   Median :  13.50  
                    Mean   : 22457   Mean   : 5383.4   Mean   : 107.03  
                    3rd Qu.: 33378   3rd Qu.: 8298.5   3rd Qu.:  98.75  
                    Max.   :112186   Max.   :32646.0   Max.   :2040.00  
      Car           PTransit         Other           Distance     
 Min.   :    0   Min.   :    0   Min.   :   0.0   Min.   : 6.835  
 1st Qu.: 3243   1st Qu.:  249   1st Qu.:   2.0   1st Qu.: 9.539  
 Median : 9008   Median : 1057   Median :  44.0   Median :10.323  
 Mean   :13289   Mean   : 3474   Mean   : 203.4   Mean   :11.139  
 3rd Qu.:21249   3rd Qu.: 4853   3rd Qu.: 281.5   3rd Qu.:12.097  
 Max.   :52631   Max.   :41672   Max.   :2391.0   Max.   :22.660  
    Duration        Car_perc      N_INDIVIDUOS     Male_perc    
 Min.   :16.30   Min.   : 0.00   Min.   : 1566   Min.   :44.61  
 1st Qu.:23.00   1st Qu.:45.40   1st Qu.:11060   1st Qu.:46.58  
 Median :24.70   Median :62.62   Median :20855   Median :47.51  
 Mean   :25.42   Mean   :59.00   Mean   :24324   Mean   :47.54  
 3rd Qu.:27.73   3rd Qu.:75.72   3rd Qu.:36079   3rd Qu.:48.29  
 Max.   :37.42   Max.   :99.27   Max.   :68649   Max.   :55.94  
    IncomeHH        Nvehicles       DrivingLic    CarParkFree_Work
 Min.   : 884.5   Min.   :1.020   Min.   :37.04   Min.   : 5.47   
 1st Qu.:1417.8   1st Qu.:1.350   1st Qu.:57.67   1st Qu.:40.39   
 Median :1594.7   Median :1.545   Median :63.00   Median :50.51   
 Mean   :1732.6   Mean   :1.530   Mean   :62.50   Mean   :49.30   
 3rd Qu.:1953.5   3rd Qu.:1.670   3rd Qu.:68.84   3rd Qu.:57.92   
 Max.   :3462.3   Max.   :2.420   Max.   :80.79   Max.   :87.60   
     PTpass      internal  Lisboa       Area_km2      
 Min.   : 0.00   Yes:118   No :188   Min.   :  1.494  
 1st Qu.:13.41   No :118   Yes: 48   1st Qu.:  5.044  
 Median :22.71                       Median : 11.598  
 Mean   :23.82                       Mean   : 25.553  
 3rd Qu.:32.94                       3rd Qu.: 28.511  
 Max.   :60.45                       Max.   :282.125  

skim(data) # In a more organized way

Data summary

Name	data
Number of rows	236
Number of columns	20
_______________________
Column type frequency:
character	1
factor	2
numeric	17
________________________
Group variables	None

Variable type: character

skim_variable	n_missing	complete_rate	min	max	empty	n_unique	whitespace
Origin_dicofre16	0	1	6	6	0	118	0

Variable type: factor

skim_variable	n_missing	complete_rate	ordered	n_unique	top_counts
internal	0	1	FALSE	2	Yes: 118, No: 118
Lisboa	0	1	FALSE	2	No: 188, Yes: 48

Variable type: numeric

skim_variable	n_missing	complete_rate	mean	sd	p0	p25	p50	p75	p100	hist
Total	0	1	22457.00	19084.45	361.00	5917.75	17474.00	33377.50	112186.00	▇▃▂▁▁
Walk	0	1	5383.44	6224.84	0.00	763.25	3125.00	8298.50	32646.00	▇▂▁▁▁
Bike	0	1	107.03	248.65	0.00	0.00	13.50	98.75	2040.00	▇▁▁▁▁
Car	0	1	13289.24	12351.61	0.00	3243.00	9008.00	21248.75	52631.00	▇▃▂▁▁
PTransit	0	1	3473.79	5467.82	0.00	249.00	1057.00	4853.00	41672.00	▇▁▁▁▁
Other	0	1	203.45	336.04	0.00	2.00	44.00	281.50	2391.00	▇▁▁▁▁
Distance	0	1	11.14	2.66	6.84	9.54	10.32	12.10	22.66	▇▇▂▁▁
Duration	0	1	25.42	3.91	16.30	23.00	24.70	27.73	37.42	▁▇▆▂▁
Car_perc	0	1	59.00	21.56	0.00	45.40	62.62	75.72	99.27	▁▃▆▇▅
N_INDIVIDUOS	0	1	24323.80	16438.04	1566.00	11060.00	20855.00	36079.00	68649.00	▇▆▅▃▁
Male_perc	0	1	47.54	1.57	44.61	46.58	47.50	48.29	55.94	▅▇▂▁▁
IncomeHH	0	1	1732.55	453.11	884.46	1417.76	1594.73	1953.50	3462.32	▃▇▃▁▁
Nvehicles	0	1	1.53	0.24	1.02	1.35	1.54	1.67	2.42	▃▇▆▂▁
DrivingLic	0	1	62.50	8.12	37.04	57.67	63.00	68.84	80.79	▁▂▇▇▂
CarParkFree_Work	0	1	49.30	14.30	5.47	40.39	50.51	57.92	87.60	▁▃▇▇▁
PTpass	0	1	23.82	12.87	0.00	13.41	22.72	32.94	60.45	▅▇▇▂▁
Area_km2	0	1	25.55	42.58	1.49	5.04	11.60	28.51	282.13	▇▁▁▁▁

5.5 Missing data

Is there missing data (NA)? How many?

table(is.na(data))

FALSE 
 4720 

5.6 Outliers

Inspect outliers and distributions

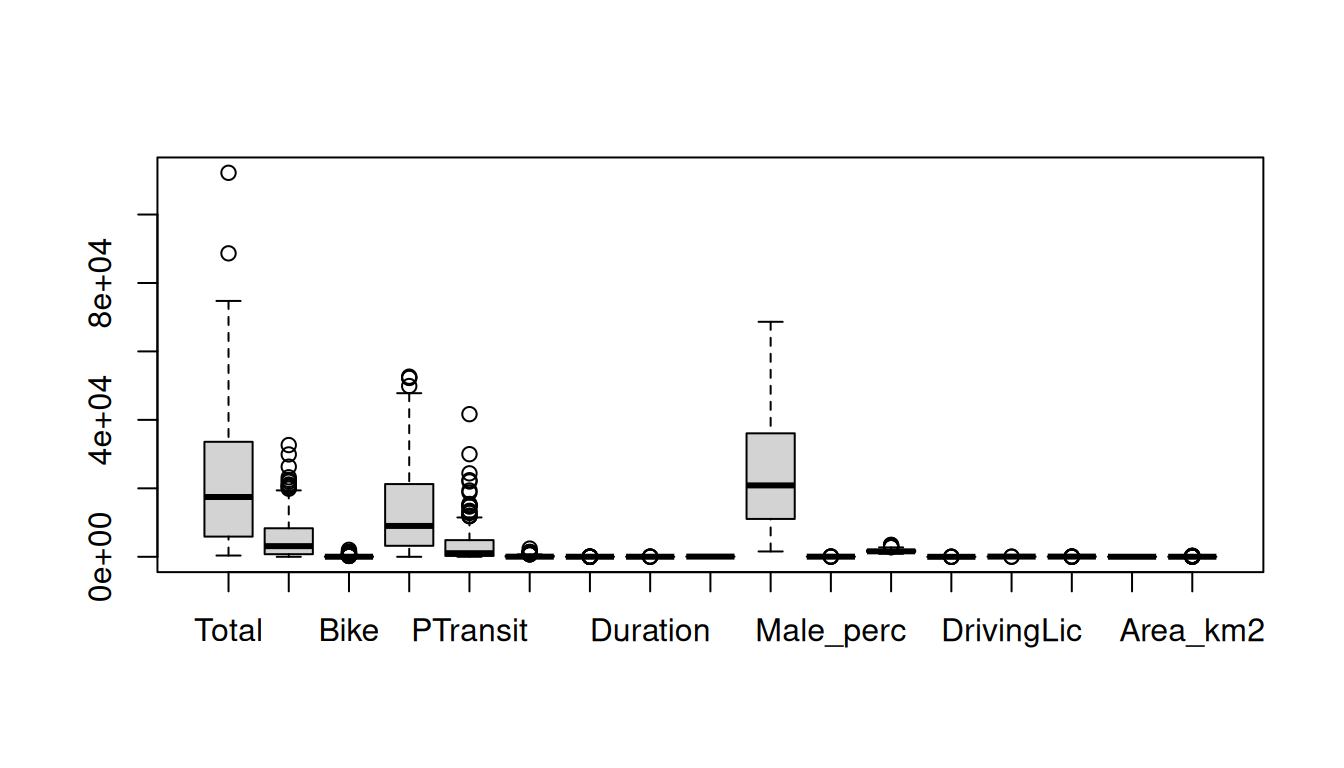
boxplot(data) # This does now work if variables are not all continuous

data_continuous = data |> select(-Origin_dicofre16, -internal, -Lisboa) # Exclude categorical variables
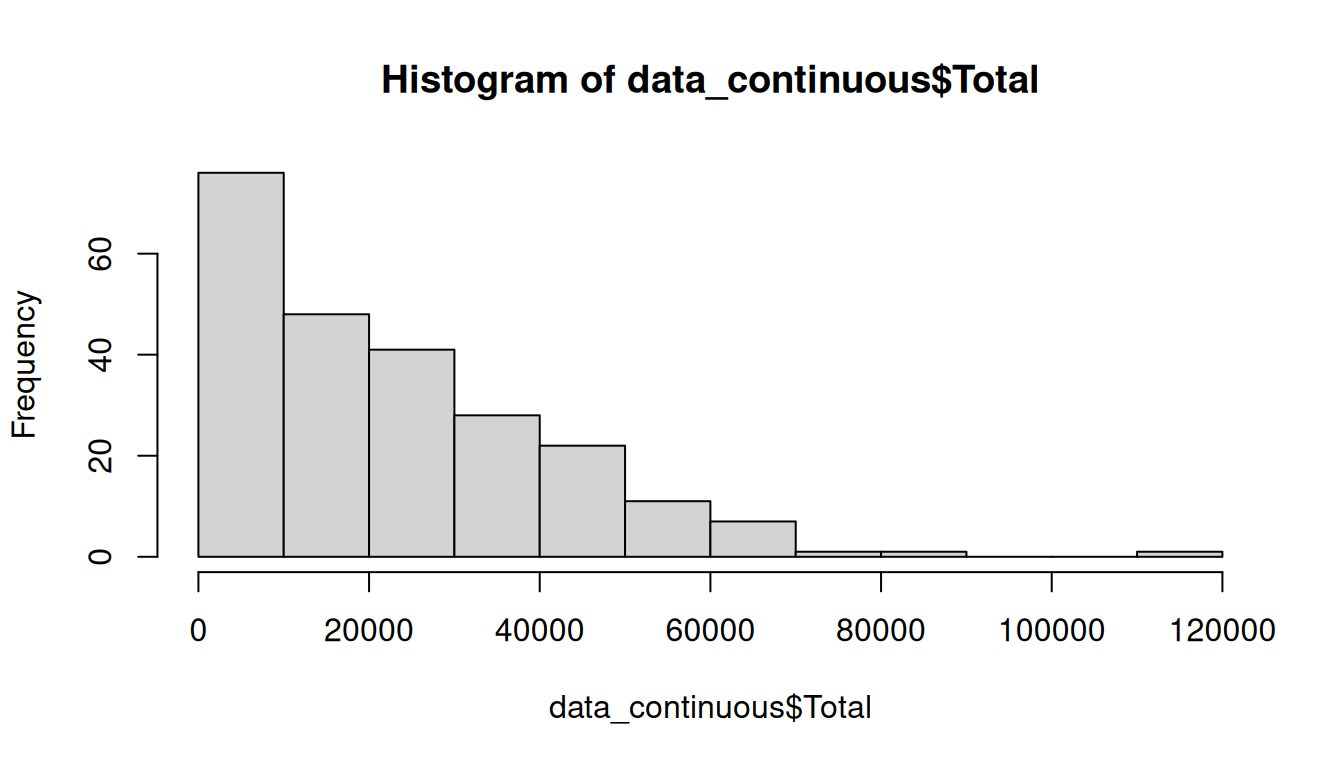
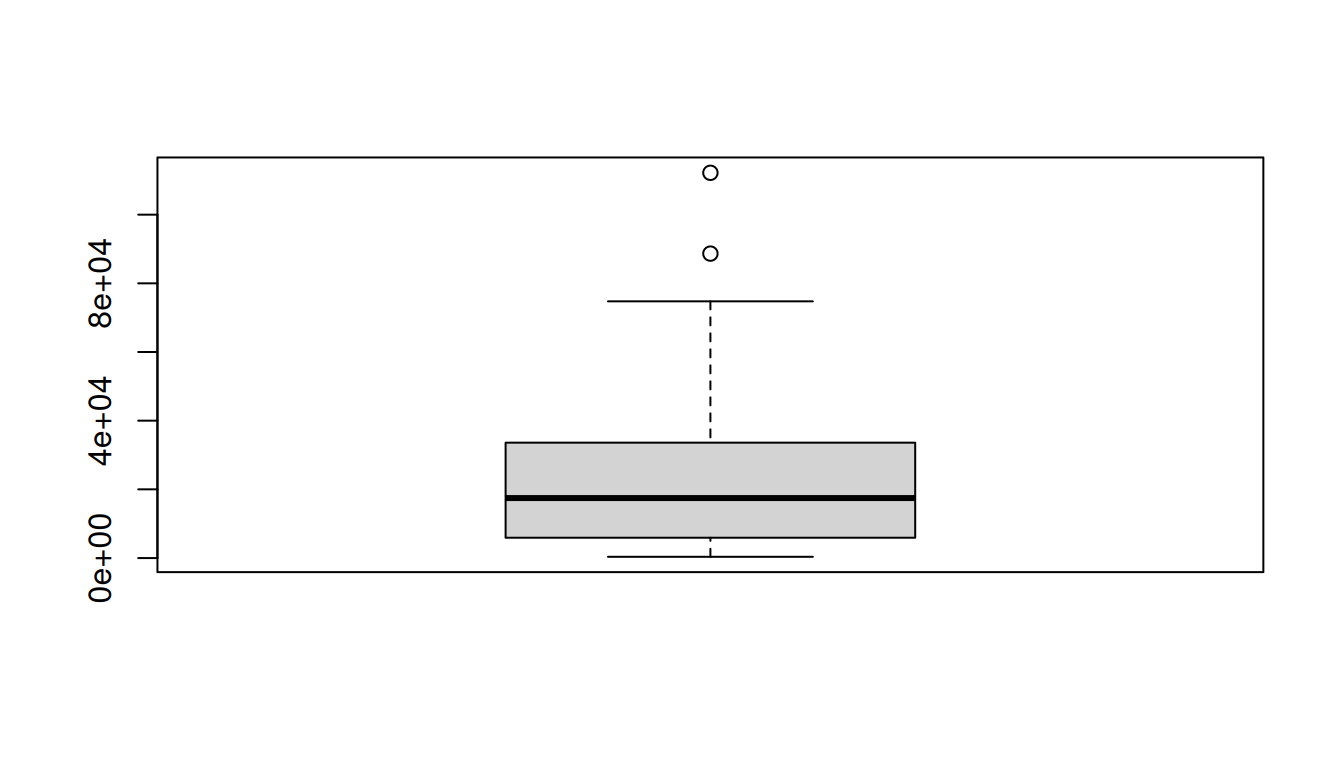
boxplot(data_continuous) # Exclude categorical variables

hist(data_continuous$Total) # histogram

boxplot(data_continuous$Total) # outliers detected

Treating outliers

Based on the theory, we can create a function to detect the outliers.

outlier = function(x) {
  q = quantile(x, probs = c(0.25, 0.75), na.rm = TRUE)  # Q1 and Q3
  caps = quantile(x, probs = c(0.05, 0.95), na.rm = TRUE) # 5th and 95th percentile
  H = 1.5 * IQR(x, na.rm = TRUE) # interquartile range
  
  case_when(
    x < (q[1] - H) ~ caps[1], # replace values that are LESS than Q1-1.5*IQR with the P5 value
    x > (q[2] + H) ~ caps[2], # replace values that are MORE than Q3+1.5*IQR with the P95 value
    TRUE ~ x # otherwise, return the original value
  )
}

Now, use it in a copy of the table

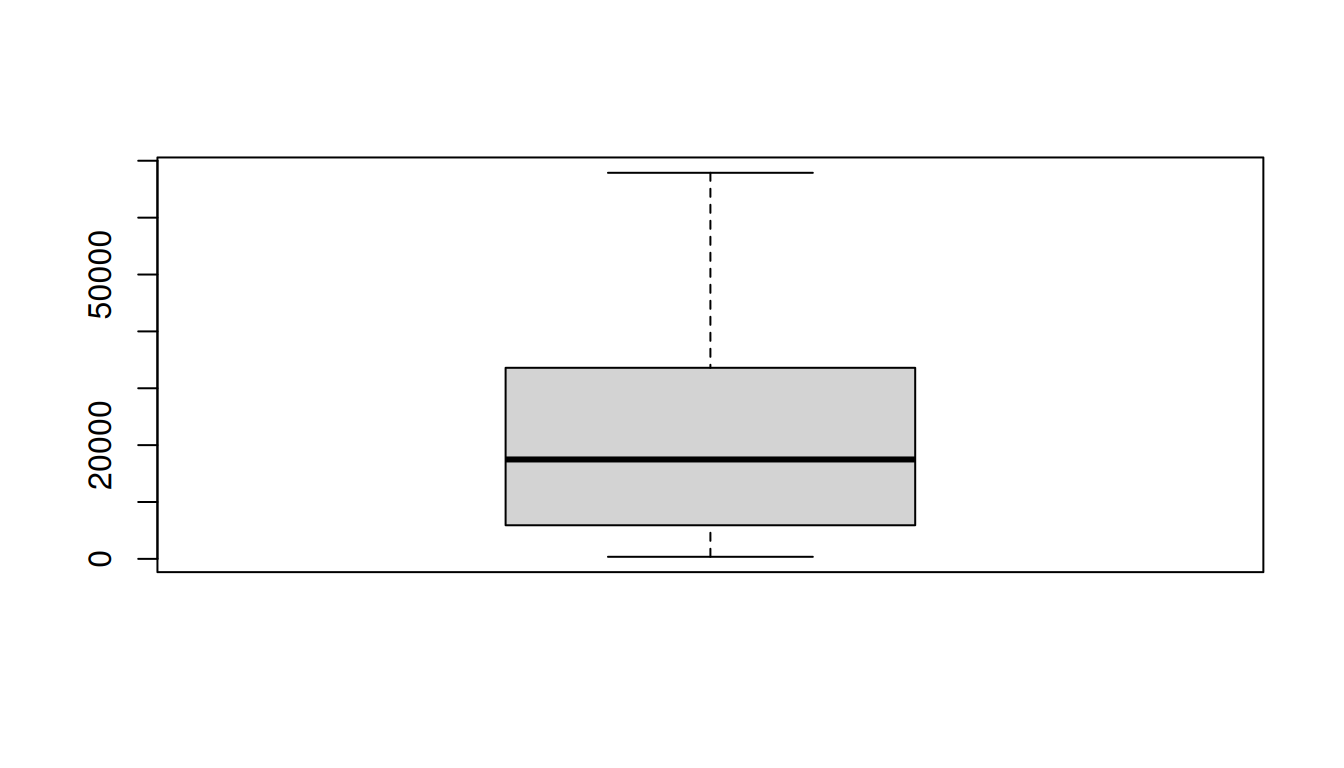
data_outliers = data_continuous # duplicate the table
data_outliers$Total = outlier(data_outliers$Total) # Use the function to the same variable

Take a look again at the boxplot

boxplot(data_outliers$Total)

Compare the variable with and without the outliers

# Mean
mean(data$Total)

[1] 22457

mean(data_outliers$Total)

[1] 22013.51

# Median
median(data$Total)

[1] 17474

median(data_outliers$Total)

[1] 17474

# Standard deviation
sd(data$Total)

[1] 19084.45

sd(data_outliers$Total)

[1] 17739.39

Note

There are many methods to treat outliers. This is just one of them.

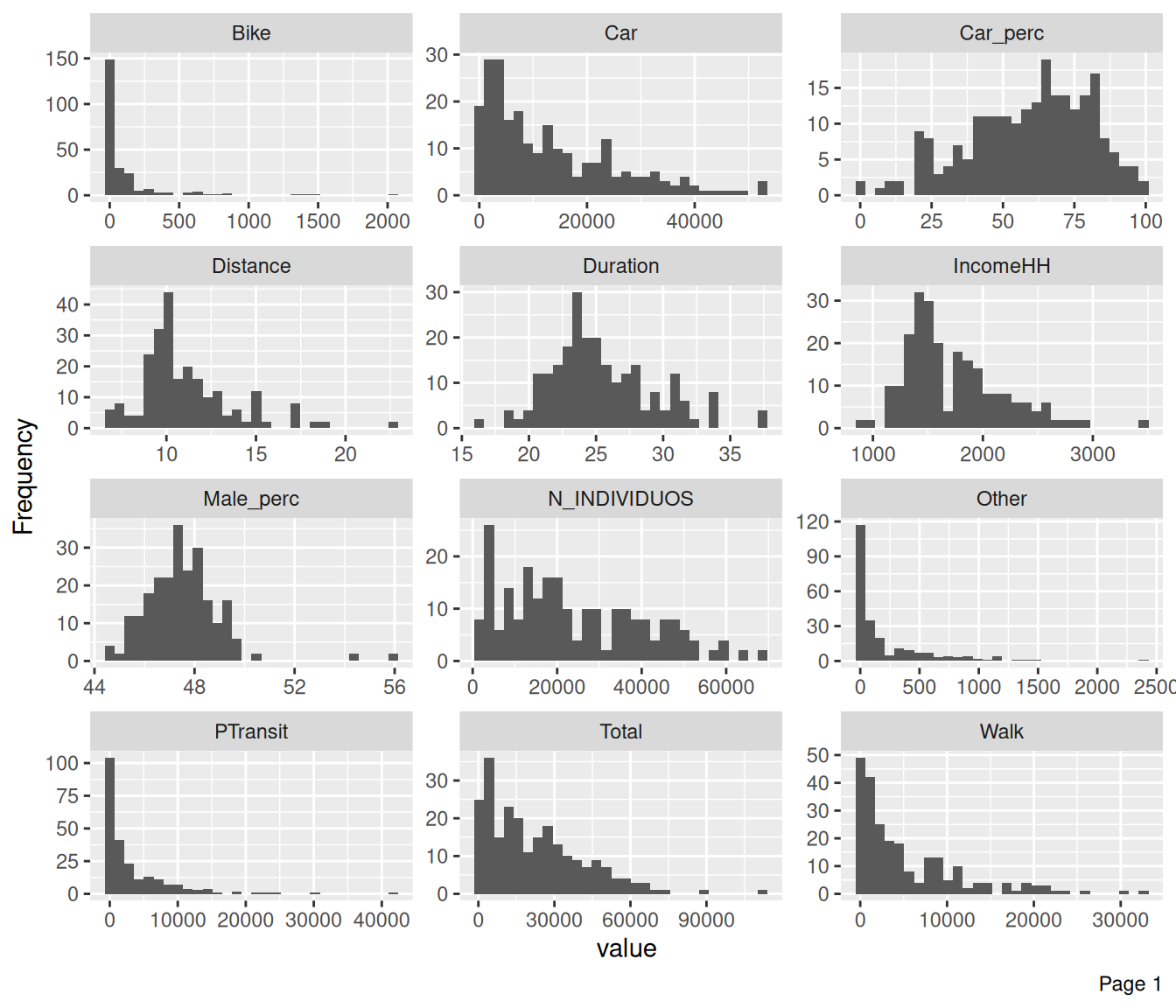
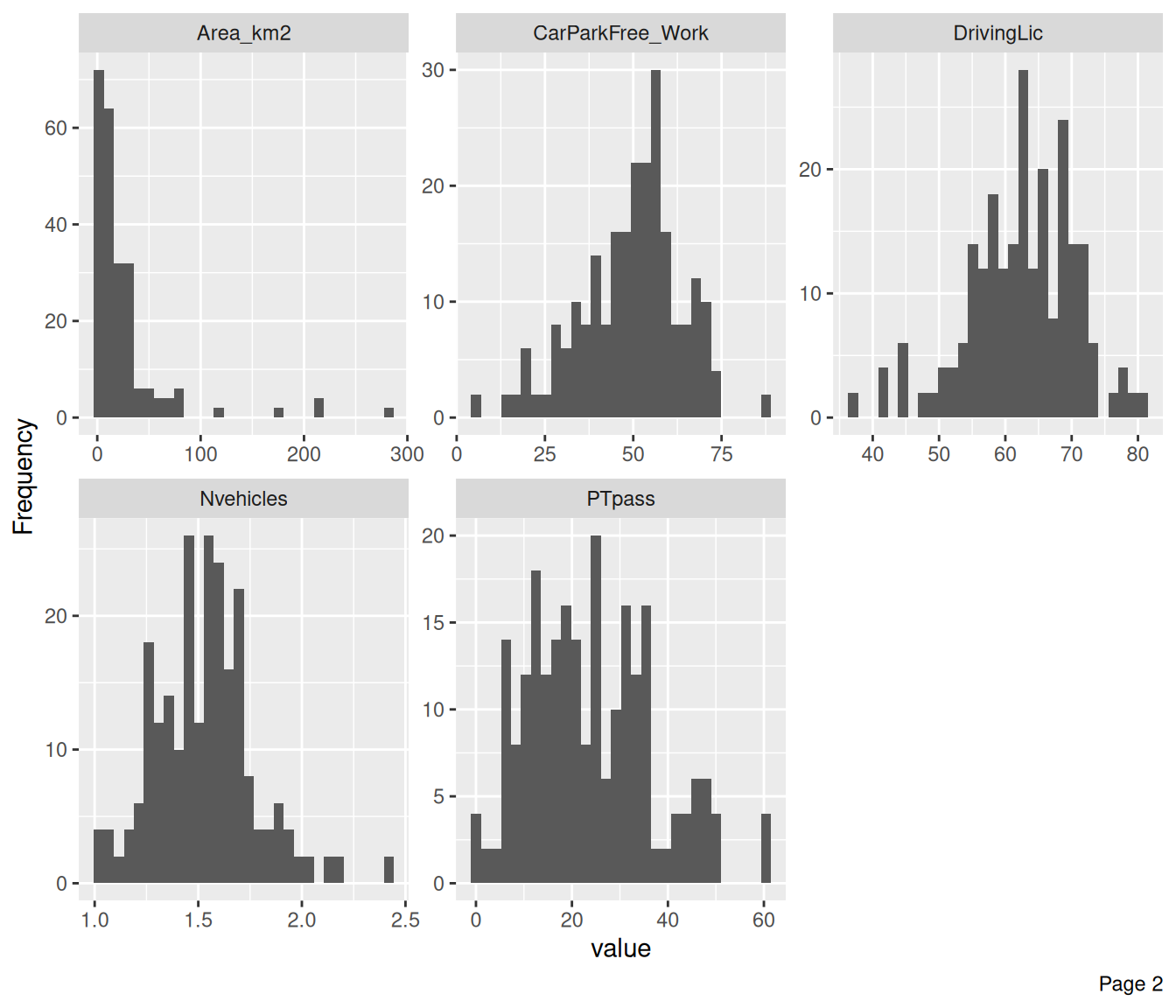
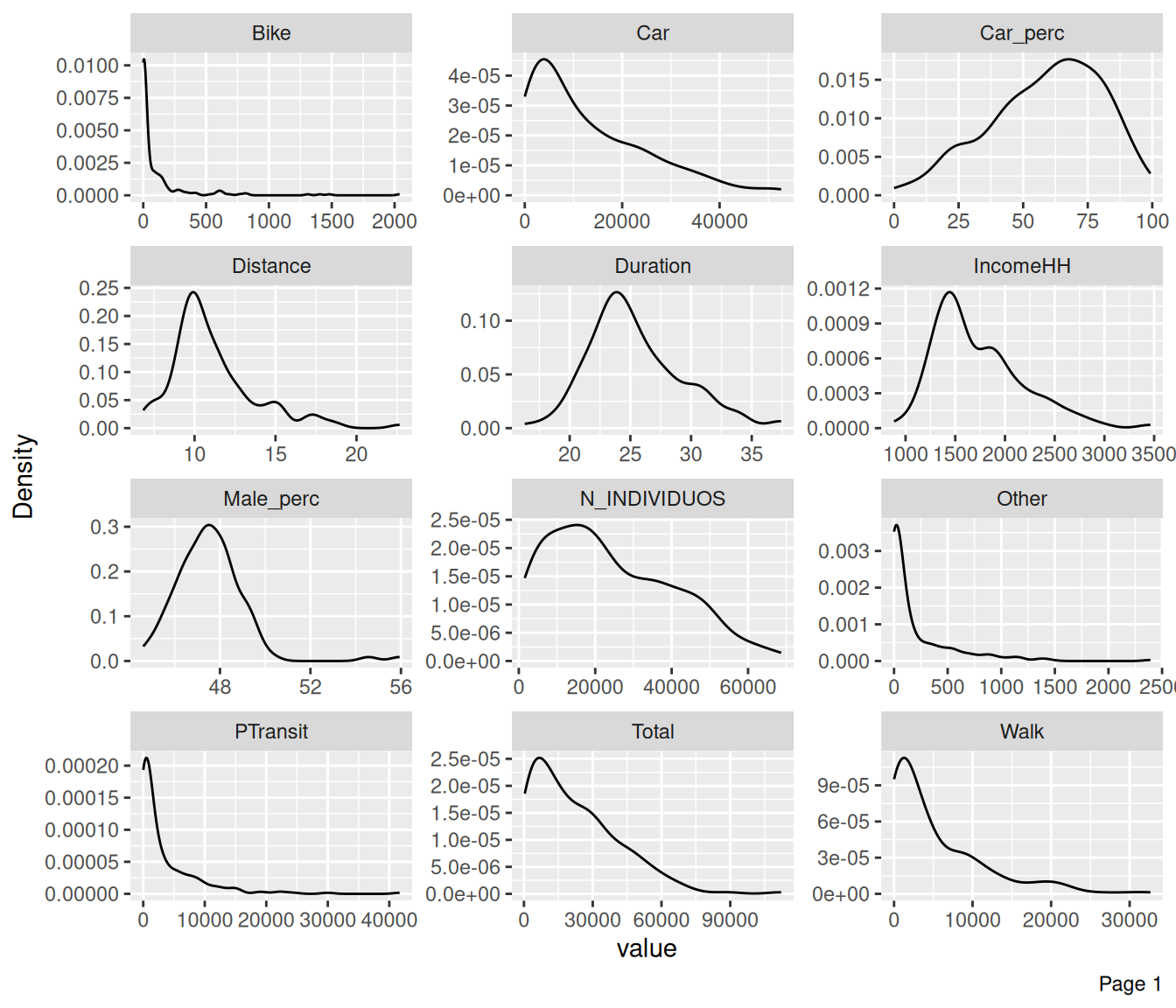
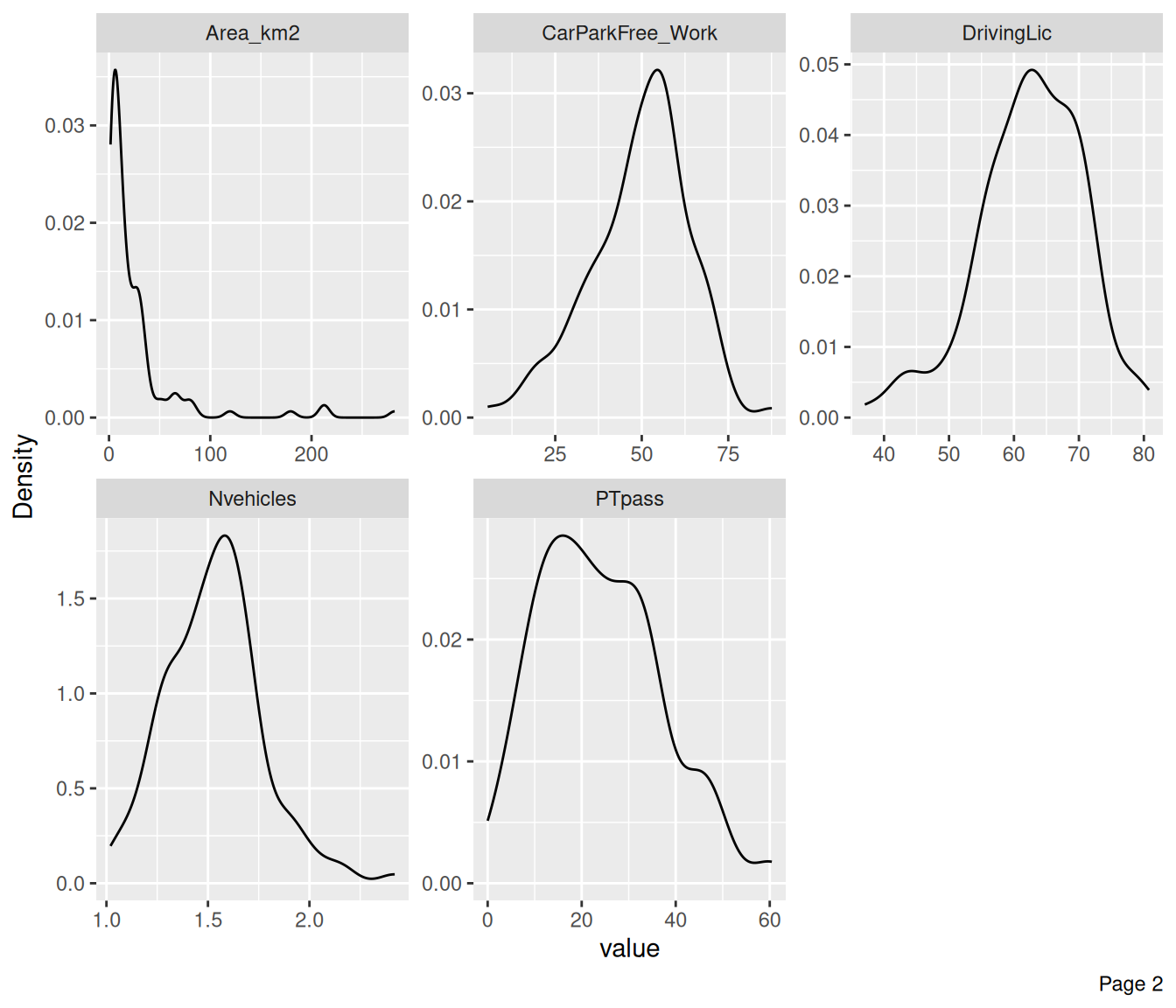
5.7 Histograms

Plot histograms of all the continuous variables

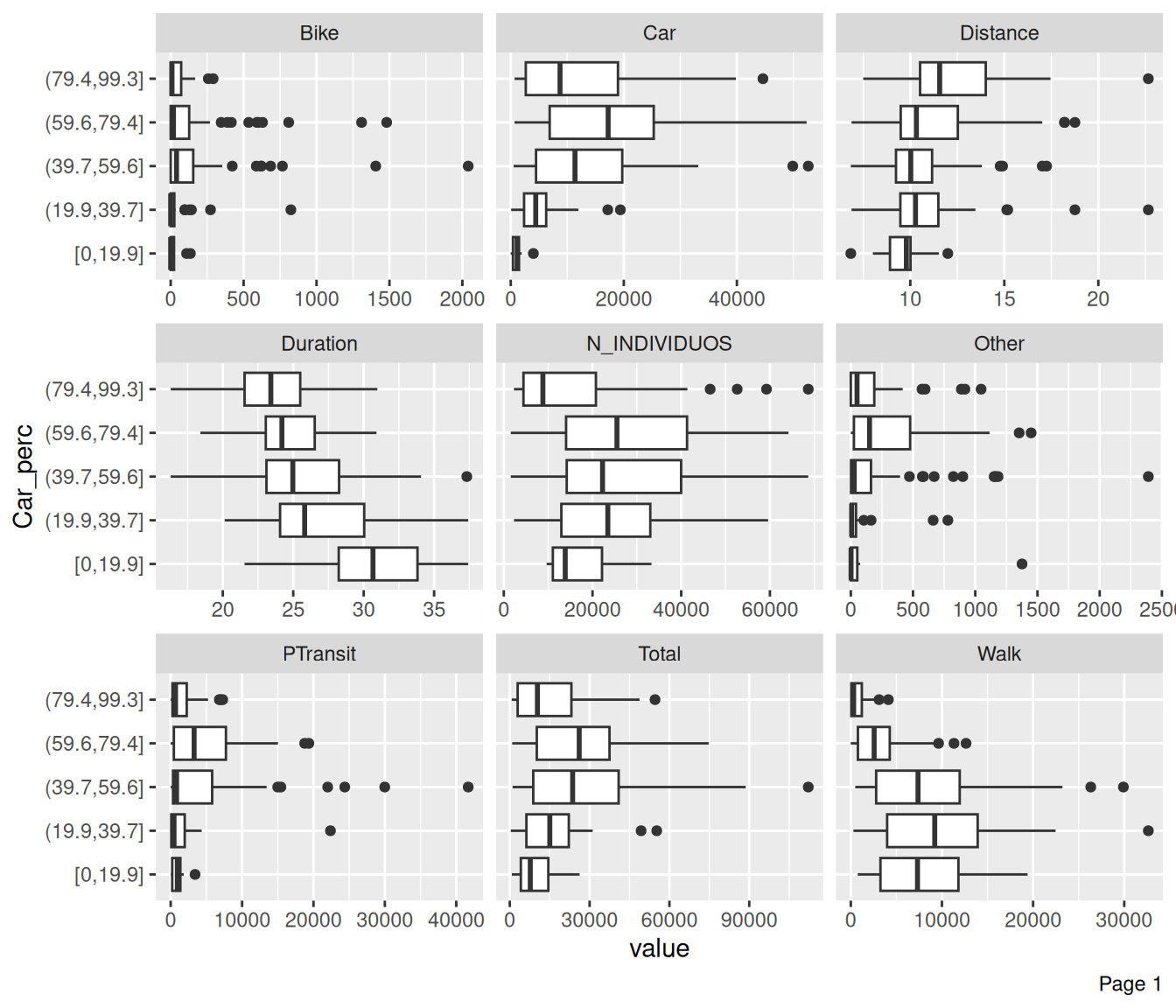
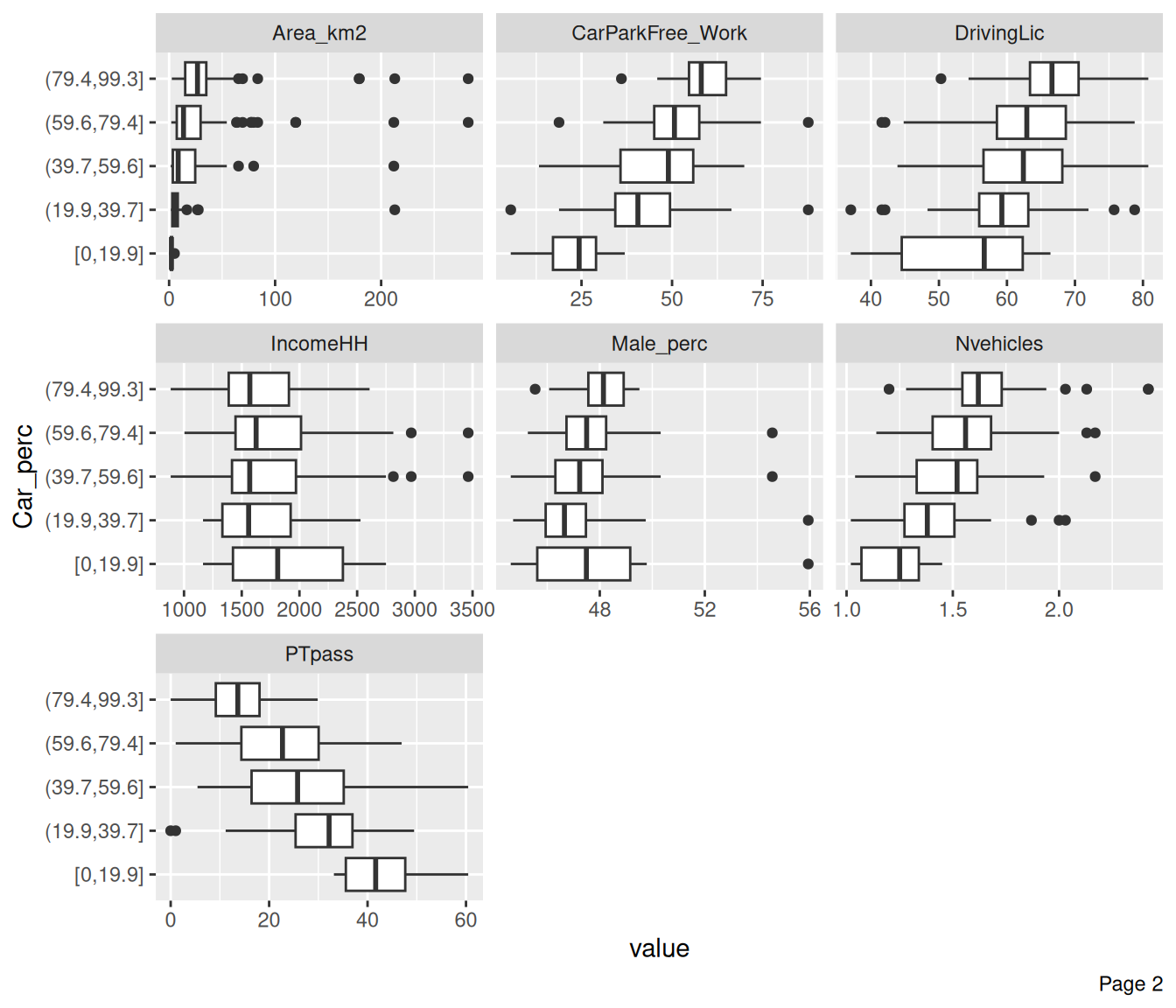
plot_histogram(data, ncol = 3) # histograms with 3 columns

plot_density(data, ncol = 3) # density plots

Check how other variables are distributed regarding Car_perc

plot_boxplot(data, by = "Car_perc", ncol = 3)

Note

When Car_perc increases, PTpass decreases.

Exercise

Try plotting the boxplots of each independent variable with Car_perc.

5.8 Correlations

Plot correlation heatmaps, between continuous variables.

# estimate correlation matrix
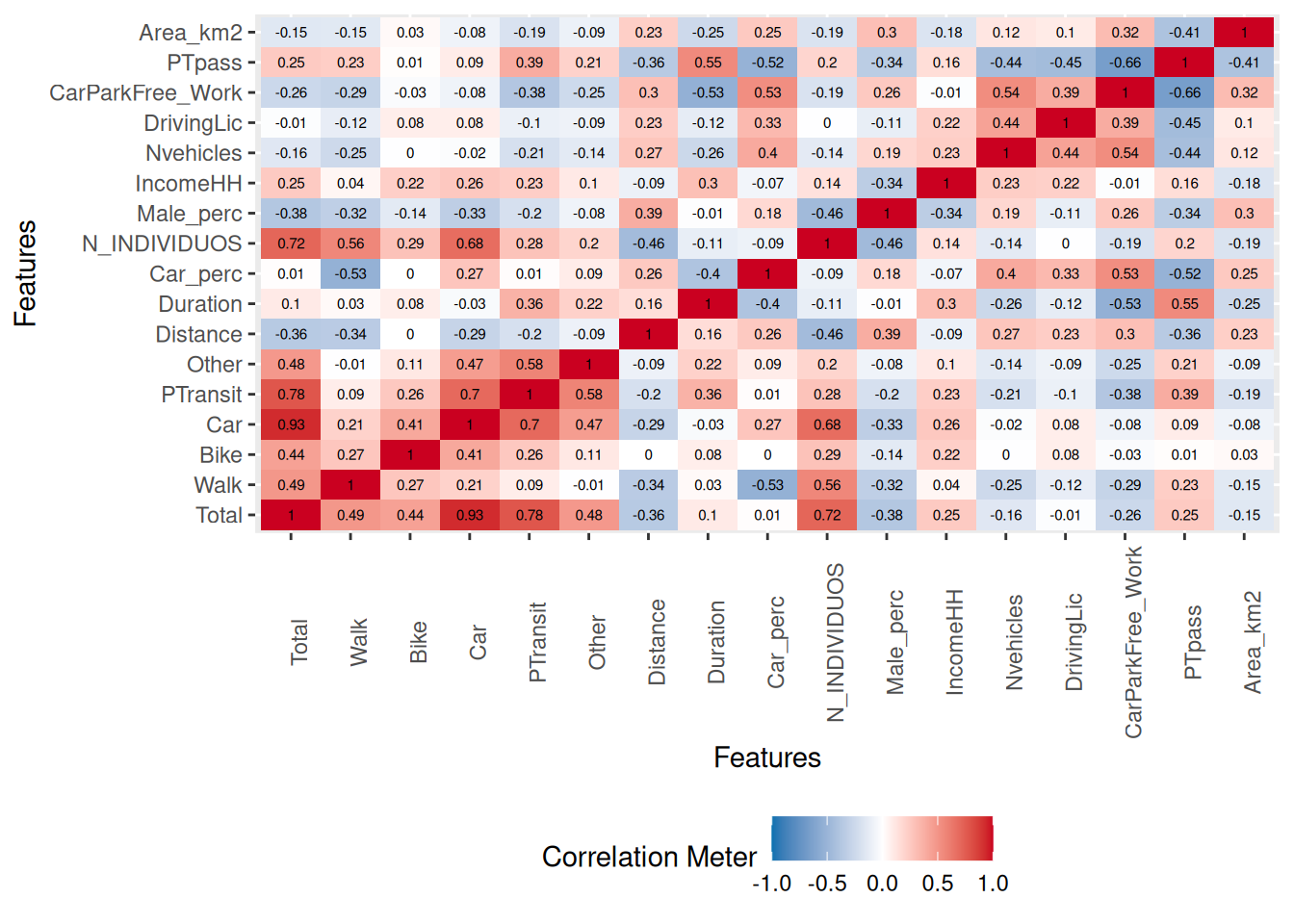
corrmat = cor(data_continuous, method = "pearson") |> round(2)
corrmat

                 Total  Walk  Bike   Car PTransit Other Distance Duration
Total             1.00  0.49  0.44  0.93     0.78  0.48    -0.36     0.10
Walk              0.49  1.00  0.27  0.21     0.09 -0.01    -0.34     0.03
Bike              0.44  0.27  1.00  0.41     0.26  0.11     0.00     0.08
Car               0.93  0.21  0.41  1.00     0.70  0.47    -0.29    -0.03
PTransit          0.78  0.09  0.26  0.70     1.00  0.58    -0.20     0.36
Other             0.48 -0.01  0.11  0.47     0.58  1.00    -0.09     0.22
Distance         -0.36 -0.34  0.00 -0.29    -0.20 -0.09     1.00     0.16
Duration          0.10  0.03  0.08 -0.03     0.36  0.22     0.16     1.00
Car_perc          0.01 -0.53  0.00  0.27     0.01  0.09     0.26    -0.40
N_INDIVIDUOS      0.72  0.56  0.29  0.68     0.28  0.20    -0.46    -0.11
Male_perc        -0.38 -0.32 -0.14 -0.33    -0.20 -0.08     0.39    -0.01
IncomeHH          0.25  0.04  0.22  0.26     0.23  0.10    -0.09     0.30
Nvehicles        -0.16 -0.25  0.00 -0.02    -0.21 -0.14     0.27    -0.26
DrivingLic       -0.01 -0.12  0.08  0.08    -0.10 -0.09     0.23    -0.12
CarParkFree_Work -0.26 -0.29 -0.03 -0.08    -0.38 -0.25     0.30    -0.53
PTpass            0.25  0.23  0.01  0.09     0.39  0.21    -0.36     0.55
Area_km2         -0.15 -0.15  0.03 -0.08    -0.19 -0.09     0.23    -0.25
                 Car_perc N_INDIVIDUOS Male_perc IncomeHH Nvehicles DrivingLic
Total                0.01         0.72     -0.38     0.25     -0.16      -0.01
Walk                -0.53         0.56     -0.32     0.04     -0.25      -0.12
Bike                 0.00         0.29     -0.14     0.22      0.00       0.08
Car                  0.27         0.68     -0.33     0.26     -0.02       0.08
PTransit             0.01         0.28     -0.20     0.23     -0.21      -0.10
Other                0.09         0.20     -0.08     0.10     -0.14      -0.09
Distance             0.26        -0.46      0.39    -0.09      0.27       0.23
Duration            -0.40        -0.11     -0.01     0.30     -0.26      -0.12
Car_perc             1.00        -0.09      0.18    -0.07      0.40       0.33
N_INDIVIDUOS        -0.09         1.00     -0.46     0.14     -0.14       0.00
Male_perc            0.18        -0.46      1.00    -0.34      0.19      -0.11
IncomeHH            -0.07         0.14     -0.34     1.00      0.23       0.22
Nvehicles            0.40        -0.14      0.19     0.23      1.00       0.44
DrivingLic           0.33         0.00     -0.11     0.22      0.44       1.00
CarParkFree_Work     0.53        -0.19      0.26    -0.01      0.54       0.39
PTpass              -0.52         0.20     -0.34     0.16     -0.44      -0.45
Area_km2             0.25        -0.19      0.30    -0.18      0.12       0.10
                 CarParkFree_Work PTpass Area_km2
Total                       -0.26   0.25    -0.15
Walk                        -0.29   0.23    -0.15
Bike                        -0.03   0.01     0.03
Car                         -0.08   0.09    -0.08
PTransit                    -0.38   0.39    -0.19
Other                       -0.25   0.21    -0.09
Distance                     0.30  -0.36     0.23
Duration                    -0.53   0.55    -0.25
Car_perc                     0.53  -0.52     0.25
N_INDIVIDUOS                -0.19   0.20    -0.19
Male_perc                    0.26  -0.34     0.30
IncomeHH                    -0.01   0.16    -0.18
Nvehicles                    0.54  -0.44     0.12
DrivingLic                   0.39  -0.45     0.10
CarParkFree_Work             1.00  -0.66     0.32
PTpass                      -0.66   1.00    -0.41
Area_km2                     0.32  -0.41     1.00

# store the results so you can call the p-value at the corrplot
res = cor.mtest(data_continuous, conf.level = .95) 

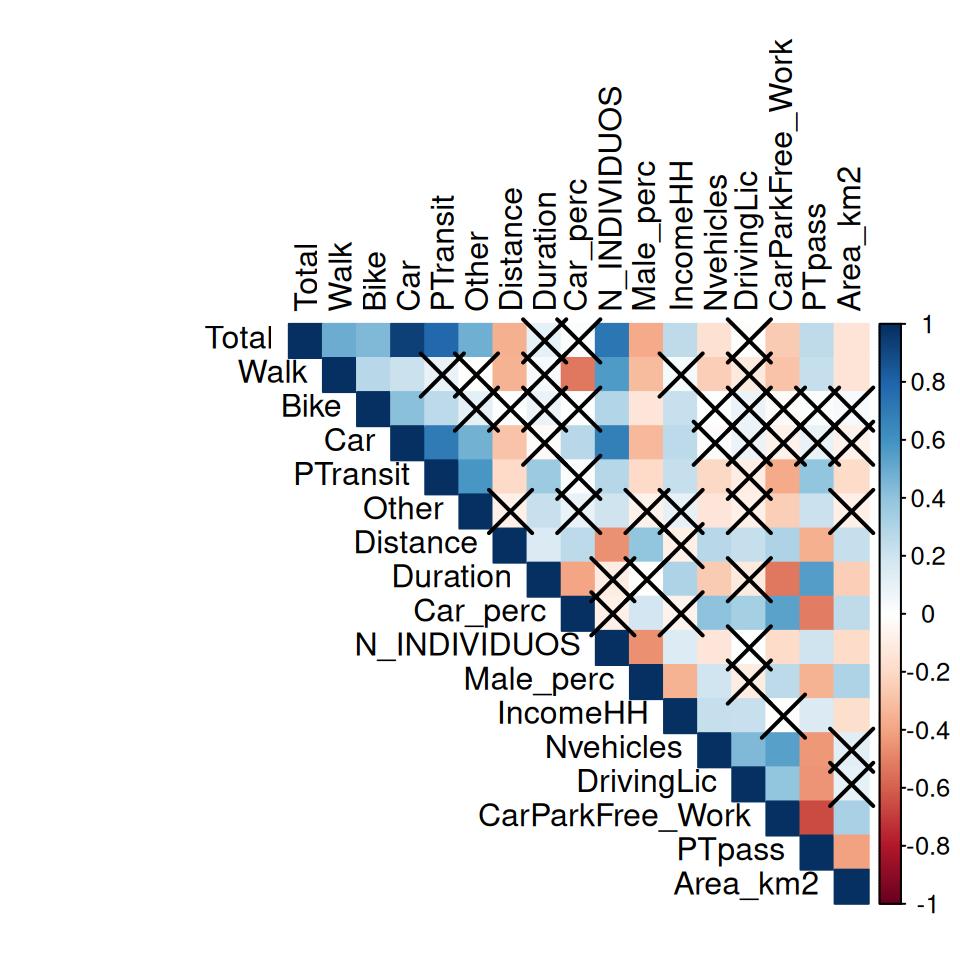
corrplot(
  corrmat,
  method = "color", # or "circle"
  p.mat = res$p,
  sig.level = 0.05,
  type = "upper", # display only the upper triangular
  # order = "hclust", # order by hierarchical clustering
  tl.col = "black" # text label color
)

Note

The pairwise correlations that are crossed are statistically not significant. The null hypothesis (H₀) is that correlation is zero. The alternative hypothesis (H_A) is that correlation is not zero.

This means that the correlations are only significant when you reject the null hypothesis (p-value < 0.05).

Other method, using the DataExplorer package

plot_correlation(data_continuous)

Check the p-value of a crossed pair correlation:

cor.test(data$IncomeHH, data$Bike)

    Pearson's product-moment correlation

data:  data$IncomeHH and data$Bike
t = 3.5261, df = 234, p-value = 0.0005074
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.09977779 0.34249284
sample estimates:
      cor 
0.2246163 

cor.test(data$IncomeHH, data$Duration)

    Pearson's product-moment correlation

data:  data$IncomeHH and data$Duration
t = 4.817, df = 234, p-value = 2.62e-06
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.1795420 0.4122446
sample estimates:
     cor 
0.300356 

cor.test(data$Distance, data$Duration)

    Pearson's product-moment correlation

data:  data$Distance and data$Duration
t = 2.4605, df = 234, p-value = 0.0146
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.0317533 0.2808153
sample estimates:
      cor 
0.1588098 

The default for cor.test is Pearson, two-sided, with a 95% confident level. Check ?cor.test for more options.

INE. 2018. “Mobilidade e Funcionalidade Do Território Nas Áreas Metropolitanas do Porto e de Lisboa: 2017.” Lisboa: Instituto National de Estatística. https://www.ine.pt/xportal/xmain?xpid=INE&xpgid=ine_publicacoes&PUBLICACOESpub_boui=349495406&PUBLICACOESmodo=2&xlang=pt.

———. 2022. “Censos 2021- XVI Recenseamento Geral da População. VI Recenseamento Geral da Habitação.” Lisboa: Instituto National de Estatística. https://censos.ine.pt/xurl/pub/65586079.

Wickham, Hadley, Mine Çetinaka-Rundel, and Garrett Grolemund. 2017. R for Data Science. 2nd ed. O’Reilly Sebastopol. https://r4ds.hadley.nz/.